Cuando no puedes simplificar un número para quitar una raíz cuadrada (o una raíz cúbica, etc.) entonces es un radical.

Ejemplo: √2 (la raíz cuadrada de 2) no se puede simplificar más así que es un radical.

Pero √4 (la raíz cuadrada de 4) sí se puede simplificar (queda 2), así que no es un radical.

 

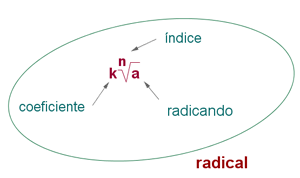
Los Radicales son expresiones de la forma:

​

​

​

​

​

En la que n Є N y a Є R; con tal que cuando a sea negativo, n ha de ser impar.

n = índice; a = radicando; m = exponente.

​

​

​

​

​

​

​

 

Un radical se puede expresar en forma de potencia, y por consiguiente, una potencia en forma de radical de la siguiente manera:

​

​

​

​

​

 

Utilizando la notación de exponente fraccionario y la propiedad de las fracciones que dice que si multiplicamos numerador y denominador por un mismo número la fracción es equivalente, obtenemos un radical equivalente al original.

​

​

​

​

​

 

Dicho de otro modo, si se multiplican o dividen el índice y el exponente de un radical por un mismo número natural, se obtiene otro radical equivalente.

Si existe un número natural que divida al índice y al exponente del radicando, se obtiene un radical simplificado.

¿Cómo reducir a índice común?

En primer lugar hallamos el mínimo común múltiplo de los índices, que será el común índice. Seguidamente, dividimos el común índice por cada uno de los índices y cada resultado se multiplica por sus exponentes correspondientes.

Ejemplo:

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

 

Para extraer factores de un radical se descompone el radicando en factores. Si:

• Un exponente es menor que el índice, el factor correspondiente se deja en el radicando.

​

​

​

​

• Un exponente es igual al índice, el factor correspondiente sale fuera del radicando.

​

​

​

​

• Un exponente es mayor que el índice, se divide dicho exponente por el índice.

• El coeficiente obtenido es el exponente del factor fuera del radicando y el resto es el exponente del factor dentro del radicando

​

​

​

​

 

Para introducir factores en un radical, los elevamos al índice correspondiente.

​

​

​

​

 

Respecto a la suma o resta de radicales, solamente pueden sumarse (o restarse) dos radicales cuando son radicales semejantes, es decir, si son radicales con el mismo índice e igual radicando.

​

​

​

​

​

​

 

Para multiplicar o dividir radicales hay que tener en cuenta si son del mismo o diferente índice. En el caso de multiplicaciones con el mismo índice, se multiplican los radicandos y se deja el mismo índice.

​

​

​

​

​

 

En el caso de la división, se dividen los radicandos y se deja el mismo índice.

​

​

​

​

 

Si por el contrario, las raíces son de distinto índice, se debe reducir a índice común y posteriormente multiplicarlas o dividirlas según sea la operación a realizar.

Cuando tenemos un radical elevado a una potencia, debemos elevar el radicando, dejando el mismo índice de la raíz.

​

​

​

​

​

 

Si por el contrario, la operación que debemos realizar es una raíz de un radical, el resultado es otro radical de igual radicando y cuyo índice es el produto de los dos índices.

​

​

​

​

​

​

 

¿En qué consiste la racionalización?

​

La racionalización de radicales consiste en quitar los radicales del denominador, lo que permite facilitar el cálculo de operaciones como la suma (o resta) de fracciones.

Podemos distinguir tres casos:

​

 

1.- Racionalización del tipo:

​

​

​

​

Se multiplica el numerador y el denominador por

​

​

​

​

​

​

​

​

 

2.- Racionalización del tipo:

​

​

​

​

​

​

Se multiplica numerador y denominador por

​

​

​

​

​

​

​

​

​

​

​

 

3.- Racionalización del tipo:

​

​

​

​

 

Y en general cuando el denominador sea un binomio con al menos un radical. Se multiplica el numerador y denominador por el conjugado del denominador. El conjugado de un binomio es igual al binomio con el signo central cambiado:

​

​

​

​

​

​

​

​

​

​

​

​

 

También tenemos que tener en cuenta que: suma por diferencia es igual a diferencia de cuadrados.

​

​

​

​

​

​

​

​

​